Active learning: asking questions and experimenting
There are many different ways of integrating the students’ experiences into math lessons. The following examples of company logos may serve as the basis for interesting observations.
Logos – abstract, simple, easily remembered
Companies spend a lot of money on concise logos. A good logo can easily be remembered and is also easy to identify. That is why generally simply structured, abstract symbols are preferred.
Are there any special criteria which ought to be fulfilled by an effective logo?
Asking questions
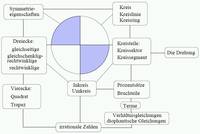
Obviously this logo contains a number of geometrical features. But the main question does not only refer to the geometry of the figure. As a start the students should be asked to make a questionnaire which would be useful for the observation of this and many other logos:
- How is the logo structured?
- Are there any symmetries?
- How much of the total area is covered by the areas of the different parts?
- Does the logo appeal to you?
- How did the logo develop?
Experimenting – Comparing – Discovering
Edgar Höniger (University of Bayreuth) gives a few more examples of questions that could be asked and he also gives a detailed description of various ways of solving problems concerning car logos.
The principal question: "What actually makes a good logo?" is closely connected with the question: Is this logo attractive? The answer to these questions will be rather subjective in many parts. But are there not any objective criteria, such as the geometry of the figure, the choice of colour, but also the connection with the information the logo is supposed to convey?
Below you can see some alternative designs which could be the basis for further discussion. A mouseclick allows the enlargement of the picture:
Dynamic logos
Do you like this example, but you doubt whether there is time to deal with it in your lessons? Try the possibilities of dynamic math software.
Math around the logo
Reflecting on the questions and answers about a logo may lead to a great variety of math problems.
The diagram on the left shows how to summarize and integrate these items. A mouseclick leads to the enlargement of the picture.
More detailed material
The example is taken from E. Höniger, Firmenlogos.The article can be downloaded here. (pdf, 241 kb)